La symétrie centrale est une notion fondamentale en géométrie qui permet de comprendre la relation entre les formes et les points de symétrie. Dans cet article, nous allons explorer en détail la symétrie centrale, les figures symétriques et les propriétés associées. Commençons par définir ce qu’est la symétrie centrale et comment elle fonctionne.
Définition de la symétrie centrale
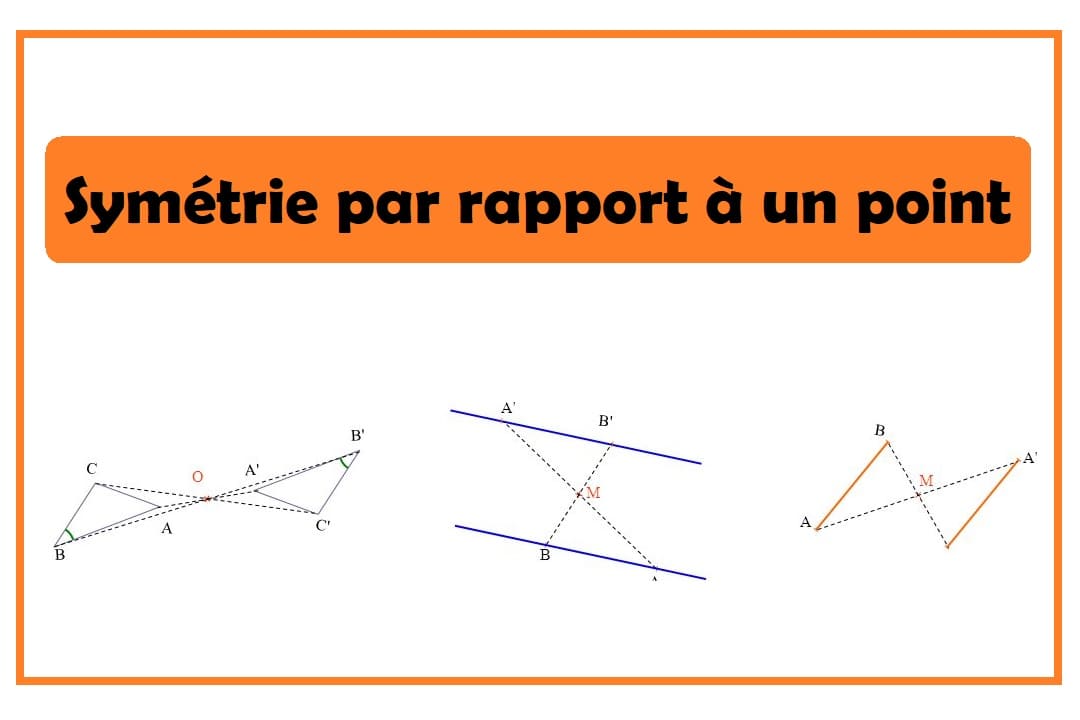
La symétrie centrale est une transformation géométrique qui implique un point central appelé « centre de symétrie ». Deux figures sont considérées comme symétriques par rapport à un point si elles peuvent être superposées par demi-tour autour de ce point. Le centre de symétrie est le point autour duquel la symétrie s’effectue.
Prenons un exemple pour mieux comprendre : considérons les figures (F) et (F’), qui sont symétriques par rapport au point O. Dans ce cas, O est le centre de symétrie.
Symétrique d’un point
Définition
Le symétrique d’un point M par rapport à un point O est un point M’ tel que le segment [MM’] a pour milieu le point O. Une remarque importante à noter est que dans le cas de la symétrie de centre O, le symétrique du point O est lui-même.
Construction du symétrique d’un point
Pour construire le symétrique M’ d’un point M par rapport à un point O, suivez ces étapes simples :
- Tracez la demi-droite [MO).
- À partir du point O, reportez la longueur MO.
- L’arc de cercle tracé coupera la demi-droite [MO) en M’.
- Cette construction garantit que le segment [MM’] est équidistant du point O.
Propriétés de la symétrie centrale
Construire le symétrique d’une figure par rapport à un point
Une propriété essentielle de la symétrie centrale est que le symétrique d’une figure par rapport à un point est une figure qui lui est parfaitement superposable. Cela signifie que les deux figures ont la même forme et les mêmes mesures.
Symétrique d’une droite
- La symétrie centrale conserve l’alignement des points.
- Le symétrique d’une droite par rapport à un point est une droite parallèle à la première.
- Le symétrique d’une demi-droite par rapport à un point est une demi-droite également parallèle, mais en sens contraire.
- La méthode pour tracer le symétrique d’une droite implique de tracer les symétriques de deux de ses points.
Symétrique d’un segment
- Le symétrique d’un segment par rapport à un point est un segment de même longueur et parallèle au segment d’origine.
- La symétrie centrale conserve les longueurs.
- Pour tracer le symétrique d’un segment, il suffit de tracer les symétriques de ses extrémités.
Voir aussi | Médiatrice d’un segment 6ème : cours et exercices
Symétrique d’un cercle
Le symétrique d’un cercle par rapport à un point est un autre cercle ayant le même rayon. Les centres de ces deux cercles sont également symétriques par rapport à ce point. Pour tracer le symétrique d’un cercle, il suffit de tracer le symétrique de son centre tout en conservant le rayon initial.
Symétrique d’un polygone
Dans le cas de la symétrie de centre O, le symétrique d’un polygone ABCDE est le polygone RSTUV. Cette symétrie garantit que les périmètres et les aires des deux polygones sont égaux. Les angles correspondants dans les deux polygones sont également symétriques, ce qui signifie que leurs mesures sont égales.
Le Centre de symétrie
Centre de symétrie de deux figures
Le centre de symétrie d’une symétrie centrale est le point qui se trouve au milieu de tous les segments reliant deux points symétriques sur chacune des figures. Une propriété importante à retenir est que le seul point invariant dans une symétrie centrale est le centre de symétrie. Il est également intéressant de noter que la figure symétrique semble « à l’envers » car elle a subi un demi-tour.
Centre de symétrie d’une figure
Lorsque le symétrique d’une figure par rapport à un point est la figure elle-même, ce point est appelé centre de symétrie de la figure. Ce point unique laisse la figure invariante lors d’une symétrie par rapport à lui-même.
Voir aussi | Symétrie axiale CE2 : leçon, exercices et évaluation
Symétrie par rapport à un point : exercices à imprimer
Pour mieux comprendre ces concepts, prenons quelques exemples et fiches d’exercices en PDF :
Symétrie par rapport à un point CM2 : exercices à imprimer
Cette fiche d’exercice est disponible sur Ekladata, axée sur la symétrie sans l’utilisation de quadrillage. Cette fiche comprend trois exercices diversifiés, chacun accompagné de son corrigé. L’objectif principal de cette ressource pédagogique est d’aider les apprenants à développer la capacité d’identifier et de dessiner des figures symétriques de manière précise, même en l’absence de repères graphiques traditionnels.
Symétrie par rapport à un point 6ème : exercices à imprimer
Cette fiche met en avant une précieuse fiche d’exercices accessible via Mathématiques-web, centrée sur la symétrie axiale pour les élèves de sixième (6ème). La ressource offre une série d’exercices variés accompagnés de solutions, permettant aux élèves de renforcer leurs compétences en géométrie.
La construction d’images par symétrie d’axe (d) avec des outils comme la règle, le compas et l’équerre est au cœur de ces exercices interactifs en ligne. Cette opportunité de pratique soutient le développement de compétences essentielles en résolution de problèmes et en compréhension des fondamentaux de la symétrie axiale, des compétences qui trouveront des applications tout au long de leur parcours éducatif.
Symétrie par rapport à un point 5ème : exercices à imprimer
Sur la plateforme Tux Family, découvrez une ressource pédagogique riche : une fiche d’exercices complète dédiée à la symétrie par rapport à un point, conçue spécialement pour les élèves de cinquième (5ème). Cette compilation engageante des exercices offre une exploration approfondie de la symétrie, permettant aux apprenants d’acquérir une compréhension solide tout en développant leurs compétences géométriques.
Conclusion
La symétrie centrale est une notion clé en géométrie qui permet de comprendre comment les figures peuvent être superposées par demi-tour autour d’un centre de symétrie. Cette transformation géométrique conserve les formes, les mesures d’angles, les périmètres et les aires. Comprendre la symétrie centrale peut nous aider à explorer les propriétés et les relations entre différentes formes géométriques.

Laisser un commentaire