La symétrie axiale est une notion importante en géométrie qui permet de comprendre la relation entre les différentes parties d’une figure plane. Cette transformation géométrique consiste à reproduire l’effet d’un pliage ou d’un miroir, créant ainsi une image symétrique de la figure d’origine. Au CE2, les élèves sont initiés à cette notion et apprennent à reconnaître et utiliser la symétrie axiale, à trouver un axe de symétrie, à compléter une figure pour la rendre symétrique par rapport à un axe donné, et à identifier les axes de symétrie d’une figure. Ils sont également évalués sur leur capacité à appliquer ces compétences à travers des exercices pratiques. Dans cet article, nous allons explorer les leçons, exercices et évaluations de symétrie axiale pour les élèves de CE2.
Leçon de symétrie axiale ce2
La symétrie axiale se produit quand une ligne droite partage une figure en deux parties égales. On l’appelle aussi symétrie radiale, rotationnelle ou cylindrique. Cette idée est souvent utilisée dans les formes géométriques, mais on peut aussi la voir dans la nature. Par exemple, des animaux comme les papillons, les scorpions, les coccinelles et les humains peuvent avoir une symétrie axiale.
Comment trouver la symétrie axiale ?
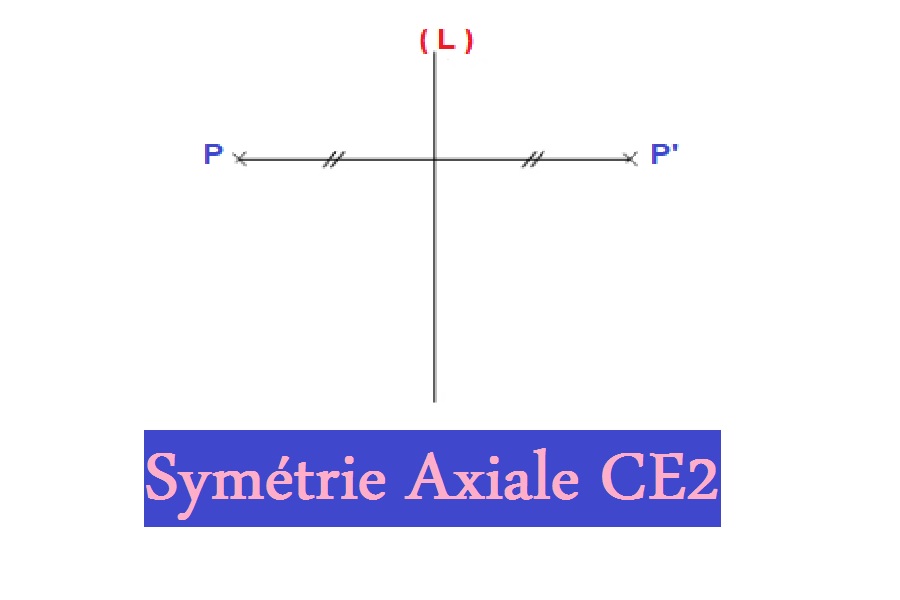
Pour trouver le symétrique axial P’ d’un point P par rapport à une droite (L), on effectue les opérations géométriques suivantes :
- La perpendiculaire à la droite (L) qui passe par le point P.
- L’intersection des deux lignes détermine un point O.
- La longueur du segment PO est mesurée, puis cette longueur est copiée sur la droite (PO) partant de O dans le sens de P à O, déterminant le point P’.
- Le point P’ est le symétrique axial du point P par rapport à l’axe (L), puisque la ligne (L) est la médiatrice du segment PP’, étant O le milieu dudit segment.
Propriétés de la symétrie axiale
- La symétrie axiale est isométrique, c’est-à-dire que les distances d’une figure géométrique et son symétrique correspondant sont conservés.
- La mesure d’un angle et celle de son symétrique sont égales.
- Le symétrique axial d’un point situé sur l’axe de symétrie est le point lui-même.
- La droite symétrique d’une droite parallèle à l’axe de symétrie est également une droite parallèle à cet axe.
- Une droite sécante à l’axe de symétrie a pour symétrique une autre droite sécante qui, à son tour, coupe l’axe de symétrie au même point de la droite d’origine.
- L’image symétrique d’une droite est une autre droite qui forme avec l’axe de symétrie un angle de même mesure que celui de la droite d’origine.
Exemples de symétrie axiale
La nature présente de nombreux exemples de symétrie axiale. On peut par exemple observer la symétrie des visages, des insectes tels que les papillons, la réflexion sur les surfaces d’eau calme et les miroirs ou les feuilles des plantes, parmi beaucoup d’autres.
Exercices sur la symétrie axiale
Exercice 1
On a le triangle de sommets A, B et C dont les coordonnées cartésiennes sont respectivement A = (2, 5), B = (1, 1) et C = (3,3). Trouver les coordonnées cartésiennes du triangle symétrique par rapport à l’axe Y (axe des ordonnées).
Solution
Si un point P a pour coordonnées (x, y), son symétrique par rapport à l’axe des ordonnées (axe Y) est P ‘= (- x, y). En d’autres termes, la valeur de son abscisse change de signe, tandis que la valeur de l’ordonnée reste la même.
Dans ce cas, le triangle symétrique dont les sommets sont A ‘, B’ et C ‘aura pour coordonnées :
A ‘= (- 2, 5) ; B ‘= (- 1, 1) et C’ = (- 3, 3) comme le montre la figure 6.
Exercice 2
Soit (L) une droite et un point A situé à gauche de cette droite. Dessinez le symétrique axial de A par rapport à (L).
Exercice 3
Soit un carré ABCD. Tracer le symétrique axial de chaque sommet par rapport à la diagonale BD.
Exercice 4
Soit un triangle ABC et un point P situé sur le côté [AB]. Tracer le symétrique axial de P par rapport à la droite passant par C et parallèle à AB.
Exercice 5
Soit un rectangle ABCD. Tracer le symétrique axial de chaque sommet par rapport à la diagonale AC.
Exercice 6
Soit un cercle de centre O et un point A situé sur ce cercle. Tracer le symétrique axial de A par rapport au diamètre qui passe par O.
Exercices et évaluations de symétrie axiale ce2 à imprimer
Les exercices de symétrie axiale sont une activité mathématique courante pour les élèves du CE2. Ces exercices sont destinés à aider les élèves à comprendre la symétrie axiale, qui est une transformation géométrique qui reflète une figure sur un axe de symétrie.
Les exercices de symétrie axiale pour les élèves du CE2 contiennent des activités telles que la reconnaissance de figures symétriques, la construction de figures symétriques, la recherche de l’axe de symétrie d’une figure donnée, la coloration de figures symétriques et la réalisation de dessins symétriques.
Exercices de symétrie axiale à imprimer
Evaluation 1 symétrie ce2 à imprimer
Evaluation 2 de symétrie axiale à imprimer

Laisser un commentaire