Les cours et exercices sur la proportionnalité en 6ème sont une étape importante pour comprendre comment les relations mathématiques peuvent être exprimées et résolues. La proportionnalité est un concept clé en mathématiques qui permet de déterminer comment deux grandeurs varient de manière similaire l’une par rapport à l’autre.
Les cours sur la proportionnalité enseignent aux élèves les méthodes pour établir des relations proportionnelles à l’aide de tableaux, de graphiques et de formules. Les exercices imprimables offrent l’occasion d’appliquer les connaissances acquises et de développer les compétences en résolution de problèmes mathématiques.
Cours proportionnalité 6ème
Un tableau de proportionnalité est un tableau à deux lignes dans lequel la deuxième ligne est obtenue en multipliant chaque nombre de la première par un même nombre appelé le coefficient de proportionnalité(qui peut être entier, décimal ou fractionnaire).
Si l’on peut passer d’une quantité à une autre en multipliant par le même nombre non nul, on dit que ces quantités sont proportionnelles. Le coefficient de proportionnalité est le nombre par lequel on multiplie pour passer de l’une à l’autre.
Tableau de proportionnalité
Si vous multipliez ou divisez le même nombre non nul sur deux lignes d’un tableau, vous avez atteint la proportionnalité.
Les tableaux suivants sont-ils des tableaux de proportionnalité ?
Tableau 1

Calculons les rapports :
4/1 = 4 , 12/3 = 4 , 28/7 = 4 , 40/10 = 4
Les rapports sont égaux donc c’est un tableau de proportionnalité.
Le coefficient de proportionnalité vaut 4.
Tableau 2
| 2 | 5 | 8 | 10 |
| 8 | 20 | 35 | 40 |
Calculons les rapports :
8/2 = 4 , 20/5 = 4 , 35/8 = 4,3 , 40/10 = 4
Les rapports ne sont pas égaux donc ce n’est pas un tableau de proportionnalité.
Linéarité
Les opérations que l’on effectue sur la première ligne d’un tableau se retrouvent dans la deuxième ligne.
Exemple
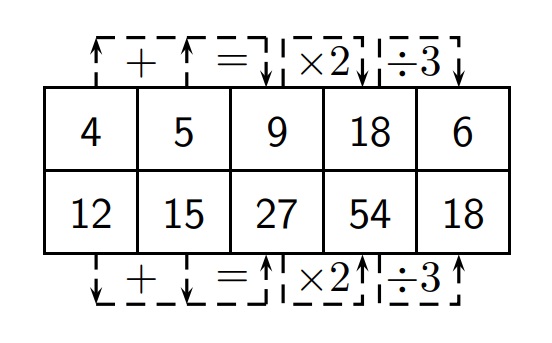
Dans ce tableau, dans la première ligne on peut dire que 4 + 5 = 9.
Dans la ligne du dessous, on a également 12 + 15 = 27.
De même, on a 9 × 2 = 18 et dessous 27 × 2 = 54,
enfin, 18 ÷ 3 = 6 et 54 ÷ 3 = 18
Règle de trois
Dans un tableau de proportionnalité, les produits « en diagonale » (ou produits en croix sont deux à deux égaux. Ceci permet de déterminer une quatrième proportionnelle.
Exemple
| 4 | 5 |
| 8 | 10 |
Dans le tableau de proportionnalité, on a l’égalité
4×10 = 8×5.
- Exemple
| 3 | 4 |
| 6 | x |
Dans le tableau de proportionnalité, on a l’égalité
3 × x = 6×4.
On calcule la donnée manquante par le calcul :
X = ( 6×4 ) ÷3
= 24÷3
= 8
Télécharger cours proportionnalité 6ème PDF
Proportionnalité 6eme : exercice en PDF
Voici des exercices sur la proportionnalité pour les élèves de 6ème en PDF :
Fichier 1
Ce fichier comprend des exercices variés sur la proportionnalité. Il comprend les questions suivantes :
- Compléter les tableaux de proportionnalité
- Les tableaux suivants sont-ils des tableaux de proportionnalité? Justifie
- Compléter les tableaux de proportionnalité en effectuant des opérations sur les colonnes
- Compléter et utiliser le tableau pour répondre
- Proportionnalité ou pas?
Conclusion
En conclusion, les cours et exercices sur la proportionnalité en 6ème sont une étape essentielle pour développer les compétences en mathématiques des élèves. En comprenant comment les grandeurs peuvent varier de manière proportionnelle, les élèves peuvent aborder avec confiance des problèmes mathématiques plus complexes à mesure qu’ils avancent dans leur parcours scolaire.
Les exercices imprimables permettent de renforcer ces compétences en fournissant des opportunités pour pratiquer et améliorer les compétences en résolution de problèmes. En fin de compte, les cours et exercices sur la proportionnalité en 6ème sont une étape clé pour garantir la réussite future des élèves en mathématiques.


Laisser un commentaire