Vous avez du mal à maîtriser le concept de proportionnalité en mathématiques ? Ne cherchez plus ! Dans cet article, nous allons explorer des cours et des exercices sur la proportionnalité de 5ème année qui vous permettront de comprendre ce concept fondamental en un rien de temps.
La proportionnalité est une compétence cruciale qui sous-tend de nombreux concepts mathématiques, notamment les rapports, les fractions et les pourcentages. En améliorant votre compréhension de la proportionnalité, vous serez mieux équipé pour résoudre des problèmes mathématiques plus complexes à l’avenir.
Cours sur la proportionnalité 5ème
Si une valeur est obtenue en multipliant une autre valeur par un nombre constant, alors ces deux valeurs sont proportionnelles. Un tableau présentant deux quantités proportionnelles s’appelle un tableau de proportionnalité.
Par exemple, un épicier qui vend des mandarines au prix de 1,6 € le kilogramme est un exemple de proportionnalité.
Voici le tableau de proportionnalité :
| Masse acheté (en €) | 1 | 2 | 5 | 10 | 20 |
| Prix payé (en €) | 1,6 | 3,2 | 8 | 16 | 32 |
On obtient le prix à payer en multipliant la masse des mandarines achetée par 1,6. Donc, le prix payé est proportionnel à la masse des mandarines achetées.
Comment reconnaître un tableau de proportionnalité ?
Pour identifier un tableau de proportionnalité, il est possible de déterminer les rapports entre les nombres de la deuxième ligne et les nombres correspondants de la première ligne. Le coefficient de proportionnalité peut être identifié en définissant le rapport commun.
Exemple
| Nombre de livres | 3 | 5 | 8 | 10 |
| Prix payé en (en€) | 15 | 25 | 40 | 50 |
Justifier que le tableau ci-dessus est un tableau de proportionnalité. Quel est le coefficient de proportionnalité ?
Réponse
15 / 3 = 5 ; 25 / 5 = 5 ; 40 / 8 = 5 ; 50 / 10 = 5
Les quotients sont égaux, donc, le tableau est un tableau de proportionnalité et le coefficient de proportionnalité est 5.
Quatrième proportionnelle
Dans une proportionnalité à quatre cases, si trois valeurs sont connues, alors on peut trouver la quatrième proportionnelle en utilisant la règle de proportionnalité.
La règle de proportionnalité énonce que dans un tableau de proportionnalité, le quotient de chaque terme de la première colonne par le terme correspondant de la deuxième colonne est égal au quotient de chaque terme de la troisième colonne par le terme correspondant de la quatrième colonne.
Ainsi, si l’on connaît trois des quatre termes, on peut utiliser la règle de proportionnalité pour trouver la quatrième proportionnelle.
Par exemple, si les trois premiers termes sont 2, 4 et 6, alors la quatrième proportionnelle sera 12, car 2/4 = 6/12.
| 2 | 4 |
| 6 | ? |
Réponse
| 2 | 4 |
| 6 | 12 |
Le pourcentage
Un pourcentage est une façon de représenter une proportion en la mettant sous forme de fraction dont le dénominateur est 100. Par exemple, si un yaourt contient 12 % de fruits, cela signifie que pour 100 g de yaourt, il y a 12 g de fruits.
Si on sait la quantité de fruits dans un pot de yaourt, on peut déterminer le pourcentage de fruits en utilisant une des deux méthodes suivantes : diviser la quantité de fruits par la masse totale du yaourt et multiplier le résultat par 100, ou utiliser la proportion de pourcentage pour calculer la quantité de fruits dans le yaourt.
Dans le troisième exemple, si un pot de yaourt de 250 g contient 15 % de fruits, cela signifie que la masse de fruits dans le yaourt est de 30 g, ce qui peut être calculé en multipliant 12 % de 250 g par 2, ou en utilisant la proportion de pourcentage pour calculer la masse de fruits dans le pot.
Exemple :
| Masse de fruit (en g) | 64 | ? |
| Masse du yaourt (en g) | 160 | 100 |
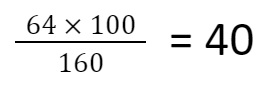
Dans ce pot de yaourt, il y a 40 % de fruits.
Echelle
Lorsqu’un plan est dessiné à l’échelle, les longueurs sur le plan sont proportionnelles aux longueurs réelles. L’échelle d’un plan est définie comme le quotient d’une longueur sur le plan par la longueur réelle correspondante, exprimées dans la même unité. On peut l’exprimer avec la formule suivante :
échelle = longueur sur le plan / longueur réelle
Par exemple, si une carte est à l’échelle de 1/2 500 000 et que la distance entre deux villes A et B est de 3 cm sur la carte, la distance réelle entre les deux villes est de 75 km. On peut trouver cette distance en multipliant la distance sur la carte par l’échelle de la carte, qui est le facteur de conversion entre les distances sur la carte et les distances réelles.
Dans un autre exemple, si une rue de 80 m est représentée par 3,2 cm sur un plan, on peut trouver l’échelle du plan en utilisant la formule d’échelle. Dans ce cas, l’échelle est de 1/2500, ce qui signifie qu’une distance de 1 cm sur le plan correspond à une distance de 2500 cm dans la réalité.
Exercices sur la proportionnalité 5ème avec corrigé
Voici des exercices corrigés sur la proportionnalité pour les élèves de cinquième :
Exercice 1
Dans une boulangerie, des croissants sont vendus par sachet. Voici les prix pratiqués.
Ce tableau est-il de proportionnalité ? Justifier la réponse.
| Nombre de croissants | Prix (en euros) |
|---|---|
| 1 | 0,80 |
| 2 | 1,60 |
| 3 | 2,40 |
| 4 | 3,20 |
| 5 | 4,00 |
Corrigé :
Ce tableau n’est pas de proportionnalité car le rapport entre le nombre de croissants et le prix ne reste pas constant.
En effet, pour deux sachets, le prix est de 1,60 €, alors que pour quatre sachets, le prix est de 3,20 €, soit deux fois plus cher.
Par conséquent, le tableau n’est pas de proportionnalité.
Exercice 2
Le prix de l’abonnement à ce journal est-il proportionnel à la durée d’abonnement ?
| Durée d’abonnement (en mois) | Prix (en euros) |
|---|---|
| 1 | 6 |
| 3 | 15 |
| 6 | 30 |
| 12 | 60 |
Corrigé :
Ce tableau est de proportionnalité car le rapport entre le prix et la durée d’abonnement reste constant.
En effet, le prix est multiplié par 3 lorsque la durée est multipliée par 3.
Par conséquent, le prix de l’abonnement à ce journal est proportionnel à la durée d’abonnement.
Exercice 3
Recopier et compléter ce tableau de proportionnalité.
| Nombre de kilogrammes | Prix (en euros) |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | |
| 4 |
Corrigé :
| Nombre de kilogrammes | Prix (en euros) |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
Exercice 4
Un camion peut transporter 5000 kg de marchandise.
- Combien de camions sont nécessaires pour transporter 200 tonnes de marchandise ?
- Si on a besoin de transporter 35000 kg de marchandise, combien de camions sont nécessaires ?
Exercice 5
Un appareil photo coûte 240 €. Pour l’acheter, Jules a économisé 50 € par mois pendant un certain temps.
- Combien de mois a-t-il dû économiser pour pouvoir acheter l’appareil photo ?
- Si Jules avait économisé 75 € par mois, combien de mois aurait-il dû économiser pour acheter l’appareil photo ?
Corrigé
- Il faut 200 000 kg / 5000 kg = 40 camions.
- Il faut 35 000 kg / 5000 kg = 7 camions.
Exercices sur la proportionnalité 5ème avec corrigé en PDF
Vous trouverez ci-dessous des exercices sur la proportionnalité de 5ème à imprimer :


Laisser un commentaire