Saviez-vous qu’il existe un moyen de transformer une fraction compliquée en une expression simple et facile à manipuler ? La réponse est la simplification de fractions ! En divisant le numérateur et le dénominateur par leur plus grand diviseur commun, vous pouvez réduire la fraction à sa forme la plus simple et la rendre irréductible.
La simplification de fractions est un outil essentiel en mathématiques et en sciences, mais elle peut également être utile dans la vie quotidienne pour résoudre des problèmes et faciliter la compréhension. Prêt à découvrir comment simplifier une fraction au maximum ?
Comment simplifier une fraction au maximum ?
Pour simplifier une fraction au maximum, il faut trouver le PGCD (plus grand commun diviseur) du numérateur et du dénominateur. Pour ce faire, vous pouvez dresser la liste des facteurs des deux nombres (numérateur et dénominateur) et trouver le plus grand facteur commun (PGFC).
Exemple de simplification d’une fraction : 24/36
1. Liste des facteurs :
On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
Pour 24, les facteurs sont :
1, 2, 3, 4, 6, 8, 12, 24
Pour 36, les facteurs sont :
1, 2, 3, 4, 6, 9, 12, 18, 36
2. Diviseurs communs :
Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 24 et 36. Dans notre exemple, les diviseurs communs sont :
1, 2, 3, 4, 6, 12
Notez que le plus grand diviseur commun est 12, car c’est le plus grand nombre qui divise à la fois 24 et 36 .
3. Division :
Il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 12, donc on divise le numérateur et le dénominateur par 12.
Cela donne :
24 / 36 = (24 ÷ 12) / (36 ÷ 12) = 2 / 3
Cette fraction est simplifiée au maximum, car 2 et 3 n’ont pas de diviseur commun autre que 1.
Une fois que vous avez trouvé le PGCD, vous devez diviser le numérateur et le dénominateur par ce nombre pour simplifier la fraction autant que possible. Cette opération permet d’obtenir une fraction irréductible, c’est-à-dire une fraction qui ne peut plus être simplifiée davantage.
Exemple de simplification d’une fraction : 16/24
- Liste des facteurs : On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
- Pour 16, les facteurs sont 1, 2, 4, 8 et 16
- Pour 24, les facteurs sont 1, 2, 3, 4, 6, 8, 12 et 24
- Diviseurs communs : Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 16 et 24. Dans notre exemple, les diviseurs communs sont 1, 2, 4 et 8
- Notez que le plus grand diviseur commun est 8, car c’est le plus grand nombre qui divise à la fois 16 et 24
- Division : Ensuite, il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 8, donc on divise le numérateur et le dénominateur par 8.
Cela donne :
16 / 24 = (16 ÷ 8) / (24 ÷ 8) = 2 / 3
Cette fraction est simplifiée au maximum, car 2 et 3 n’ont pas de diviseur commun autre que 1.
Exemple de simplification d’une fraction : 21/28
- Liste des facteurs : On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
- Pour 21, les facteurs sont 1, 3, 7 et 21.
- Pour 28, les facteurs sont 1, 2, 4, 7, 14 et 28.
- Diviseurs communs : Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 21 et 28. Dans notre exemple, le diviseur commun est 7.
- Notez que 7 est également le plus grand diviseur commun dans ce cas.
- Division : Ensuite, il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 7, donc on divise le numérateur et le dénominateur par 7.
Cela donne :
21 / 28 = (21 ÷ 7) / (28 ÷ 7) = 3 / 4
Cette fraction est simplifiée au maximum, car 3 et 4 n’ont pas de diviseur commun autre que 1.
En résumé, pour simplifier une fraction au maximum, vous devez trouver le PGCD du numérateur et du dénominateur, puis diviser ces nombres par ce nombre pour obtenir une fraction irréductible. Vous pouvez également utiliser la factorisation pour simplifier la fraction.
Fiches d’exercices pour simplifier une fraction en PDF
Les fiches d’exercices pour simplifier une fraction au maximum sont des outils éducatifs conçus pour aider les élèves à apprendre et à pratiquer la simplification des fractions.
Ces fiches d’exercices contiennent plusieurs types de questions, allant des questions de base aux questions plus complexes. Les questions peuvent impliquer des fractions avec des numérateurs et des dénominateurs différents, des fractions mixtes, des nombres décimaux, des pourcentages, des fractions avec des racines carrées et des exposants, et bien plus encore.
Les élèves peuvent également être invités à simplifier des fractions sous différentes formes, y compris sous forme de fractions irréductibles, sous forme de nombres décimaux ou sous forme de pourcentages.
Fiche d’exercices pour simplifier une fraction cm1
Fiche d’exercices pour simplifier une fraction cm2
Voir aussi : Comment simplifier une fraction étape par étape ?

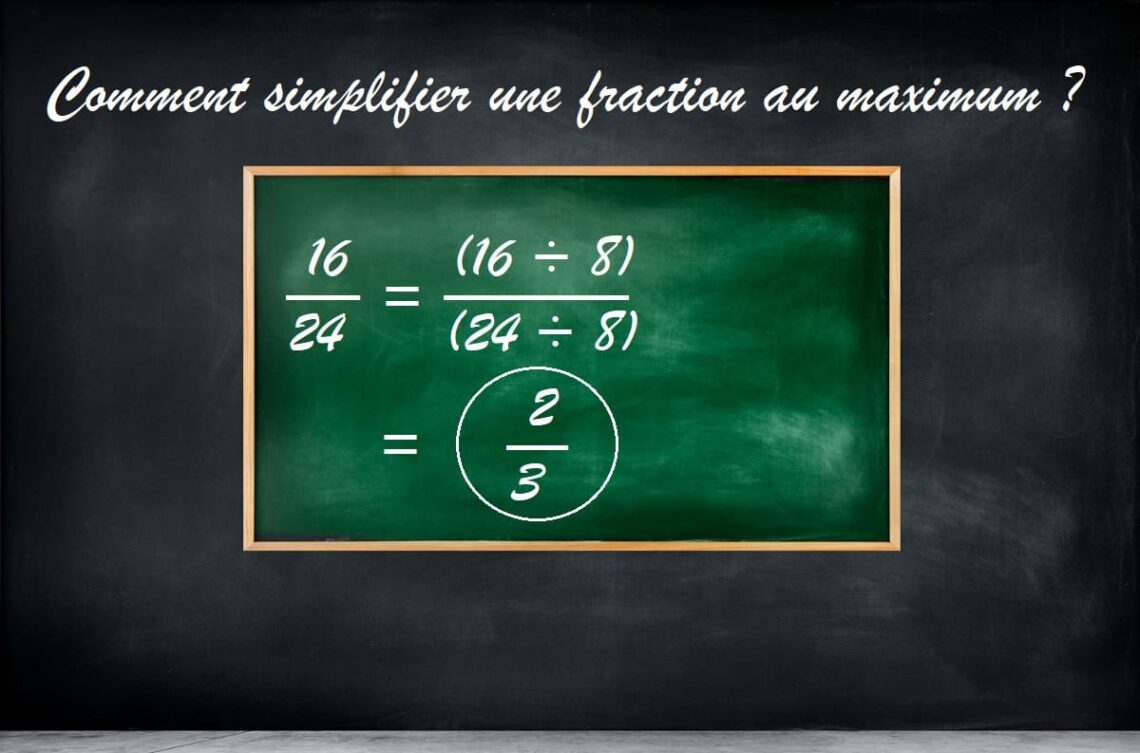
Laisser un commentaire