Simplifier une fraction, c’est la réduire à sa forme la plus simple. Pour cela, il faut que le numérateur et le dénominateur n’aient aucun facteur commun autre que 1. C’est une étape importante lorsque l’on travaille sur des problèmes de fractions. Même si on les simplifie, la valeur de la fraction ne change pas. On obtient alors une paire de fractions équivalentes entre la fraction simplifiée et la fraction d’origine. Dans cet article, nous allons découvrir ensemble comment simplifier une fraction facilement.
Comment simplifier une fraction ?
Simplifier une fraction revient à la réduire à sa forme la plus simple. Une fraction est à sa forme la plus simple si son numérateur et son dénominateur sont premiers entre eux, ou n’ont aucun facteur commun autre que 1.
La forme la plus simple d’une fraction est équivalente à la fraction initiale.
Par exemple, la fraction 3/4 est à sa forme la plus simple car 3 et 4 n’ont aucun facteur commun autre que 1. Prenons l’exemple de la fraction 8/24 et simplifions-la, étape par étape.
Simplification de fractions étape par étape
Voici un processus étape par étape pour comprendre comment simplifier une fraction. Prenons l’exemple de la fraction 8/24 et suivons les étapes ci-dessous pour comprendre comment simplifier la fraction 8/24.
- Étape 1 : Écrivez les facteurs du numérateur et du dénominateur.
Les facteurs de 8 et 24 sont :
Facteurs de 8 : 1, 2, 4 et 8 Facteurs de 24 : 1, 2, 3, 4, 6, 8, 12 et 24
- Étape 2 : Déterminez les facteurs communs du numérateur et du dénominateur.
Les facteurs communs de 8 et 24 sont 1, 2, 4 et 8.
- Étape 3 : Divisez le numérateur et le dénominateur par les facteurs communs jusqu’à ce qu’ils n’aient aucun facteur commun autre que 1.
La fraction ainsi obtenue est à sa forme la plus simple. Commençons par diviser par 2, alors 8/24 = (8/2)/(24/2) = 4/12.
Nous continuerons à diviser par 2 jusqu’à ce que nous ne puissions plus continuer. Donc, nous avons (4/2)/(12/2) = 2/6 = (2/2)/(6/2) = 1/3.
Ainsi, 1/3 est la forme la plus simple de la fraction 8/24.
Maintenant, discutons également d’une méthode facile pour simplifier les fractions. Nous pouvons rendre une fraction compliquée aussi simple que possible en suivant le processus de simplification de la fraction. Afin de trouver la forme simplifiée d’une fraction, examinons une méthode facile pour simplifier la fraction. Ici, nous avons les trois sixièmes d’une pizza.
Pourquoi dire trois sixièmes alors que vous voulez dire la moitié ?
Simplifier une fraction signifie la rendre aussi simple que possible. Un moyen rapide de trouver la forme la plus simple d’une fraction consiste à calculer le facteur commun le plus élevé. Suivez les étapes ci-dessous pour apprendre la méthode la plus courte.
- Étape 1: Écrire les facteurs du numérateur et du dénominateur.
- Étape 2: Déterminer le facteur commun le plus élevé du numérateur et du dénominateur.
- Étape 3: Diviser le numérateur et le dénominateur par leur facteur commun le plus élevé.
La fraction obtenue est alors dans sa forme la plus simple. Revenons au même problème de simplifier la fraction 8/24.
Le facteur commun le plus élevé de 8 et 24 est 8. Diviser le numérateur 8 et le dénominateur 24 par 8 nous donnera directement la forme la plus simple de la fraction, c’est-à-dire 1/3.
Ainsi, la méthode la plus courte pour réduire une fraction à sa forme la plus simple consiste à diviser le numérateur et le dénominateur par leur facteur commun le plus élevé.
Simplification de fractions avec des variables
Vous pouvez également simplifier une fraction contenant des variables dans le numérateur et le dénominateur. Utilisez la forme développée de chaque terme dans le numérateur et le dénominateur pour faciliter la simplification de la fraction avec des variables.
Prenons l’exemple de la fraction (x2y )/ (xy) à simplifier.
Exprimez le numérateur et le dénominateur sous forme de produit de variables.
(x2y) / (xy) = (x . x . y) / (x . y)
Annulez les variables communes.
(x2y) / (xy) = (x . x . y) / (x . y) = x
Nous espérons que la simplification de fractions avec des variables vous a été facile.
Simplification de fractions avec des exposants
Vous pouvez simplifier une fraction contenant des exposants dans le numérateur et le dénominateur. Utilisez la forme développée des exposants dans le numérateur et le dénominateur pour faciliter la simplification de la fraction avec des exposants.
Pour faciliter la lecture d’un nombre, nous utilisons parfois des exposants. Supposons que nous avons la fraction 35/32.
Nous exprimons le numérateur et le dénominateur sous forme de produit de nombres, puis annulons les nombres communs.
35 / 32 = (3 × 3 × 3 × 3 × 3) / (3 × 3) = 3 × 3 × 3 = 27
Ainsi, vous avez enfin appris la manière de simplifier des fractions avec des exposants.
Voir aussi : Comment multiplier des fractions ?
Simplification de fractions mélangées
Une fraction mélangée est un mélange d’un nombre entier et d’une fraction propre. Pour simplifier une fraction mélangée, vous devez simplifier uniquement la partie fractionnaire. Pour cela, écrivez le numérateur et le dénominateur sous forme factorisée et annulez les facteurs communs. Le résultat sera le nouveau numérateur et le nouveau dénominateur de la fraction mélangée.
Par exemple : Simplifiez la fraction mélangée 3 x 4/10 .
Pour simplifier la fraction mélangée 3 x 4/10 , simplifiez uniquement la partie fractionnaire. Écrivez le numérateur et le dénominateur de la partie fractionnaire sous forme factorisée et annulez les facteurs communs.
4/10 = (2 × 2) / (2 × 5) = 2/5
Par conséquent, la fraction mélangée 3 x 4/10 peut-être simplifiée en 3 x 2/5 .
Simplifier les fractions impropres
Les fractions impropres sont celles où le numérateur est supérieur ou égal au dénominateur. Pour simplifier les fractions impropres, nous devons les convertir en fractions mélangées, et pour cela, nous devons diviser le numérateur par le dénominateur. Ensuite, nous l’écrivons sous forme de nombre mixte en plaçant le quotient comme nombre entier, le reste comme numérateur et le diviseur comme dénominateur. Prenons l’exemple suivant pour mieux comprendre.
Par exemple, pour simplifier la fraction impropre 11/4, nous devons diviser 11 par 4 et obtenir les valeurs du quotient et du reste après la division. Lorsque nous divisons 11/4, nous obtenons 2 comme quotient et 3 comme reste. Par conséquent, la forme simplifiée de la fraction impropre 11/4 est 2 x 3/4.
Comment simplifier une fraction : exemple
Pour simplifier une fraction au maximum, il faut trouver le PGCD (plus grand commun diviseur) du numérateur et du dénominateur. Pour ce faire, vous pouvez dresser la liste des facteurs des deux nombres (numérateur et dénominateur) et trouver le plus grand facteur commun (PGFC).
Exemple de simplification d’une fraction : 24/36
1. Liste des facteurs :
On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
Pour 24, les facteurs sont :
1, 2, 3, 4, 6, 8, 12, 24
Pour 36, les facteurs sont :
Advertisement
1, 2, 3, 4, 6, 9, 12, 18, 36
2. Diviseurs communs :
Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 24 et 36. Dans notre exemple, les diviseurs communs sont :
1, 2, 3, 4, 6, 12
Notez que le plus grand diviseur commun est 12, car c’est le plus grand nombre qui divise à la fois 24 et 36 .
3. Division :
Il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 12, donc on divise le numérateur et le dénominateur par 12.
Cela donne :
24 / 36 = (24 ÷ 12) / (36 ÷ 12) = 2 / 3
Advertisement
Cette fraction est simplifiée au maximum, car 2 et 3 n’ont pas de diviseur commun autre que 1.
Une fois que vous avez trouvé le PGCD, vous devez diviser le numérateur et le dénominateur par ce nombre pour simplifier la fraction autant que possible. Cette opération permet d’obtenir une fraction irréductible, c’est-à-dire une fraction qui ne peut plus être simplifiée davantage.
Exemple de simplification d’une fraction : 16/24
- Liste des facteurs : On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
- Pour 16, les facteurs sont 1, 2, 4, 8 et 16
- Pour 24, les facteurs sont 1, 2, 3, 4, 6, 8, 12 et 24
- Diviseurs communs : Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 16 et 24. Dans notre exemple, les diviseurs communs sont 1, 2, 4 et 8
- Notez que le plus grand diviseur commun est 8, car c’est le plus grand nombre qui divise à la fois 16 et 24
- Division : Ensuite, il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 8, donc on divise le numérateur et le dénominateur par 8.
Cela donne :
16 / 24 = (16 ÷ 8) / (24 ÷ 8) = 2 / 3
Cette fraction est simplifiée au maximum, car 2 et 3 n’ont pas de diviseur commun autre que 1.
Exemple de simplification d’une fraction : 21/28
- Liste des facteurs : On dresse la liste des facteurs des deux nombres, c’est-à-dire du numérateur et du dénominateur.
- Pour 21, les facteurs sont 1, 3, 7 et 21.
- Pour 28, les facteurs sont 1, 2, 4, 7, 14 et 28.
- Diviseurs communs : Parmi ces facteurs, on recherche les diviseurs communs, c’est-à-dire les nombres qui divisent à la fois 21 et 28. Dans notre exemple, le diviseur commun est 7.
- Notez que 7 est également le plus grand diviseur commun dans ce cas.
- Division : Ensuite, il suffit de diviser le numérateur et le dénominateur par le PGCD (plus grand commun diviseur) trouvé à l’étape précédente. Dans notre exemple, le PGCD est 7, donc on divise le numérateur et le dénominateur par 7.
Cela donne :
21 / 28 = (21 ÷ 7) / (28 ÷ 7) = 3 / 4
Advertisement
Cette fraction est simplifiée au maximum, car 3 et 4 n’ont pas de diviseur commun autre que 1.
En résumé, pour simplifier une fraction au maximum, vous devez trouver le PGCD du numérateur et du dénominateur, puis diviser ces nombres par ce nombre pour obtenir une fraction irréductible. Vous pouvez également utiliser la factorisation pour simplifier la fraction.
Exercices sur la simplification des fractions
Vous trouverez ci-dessous des fiches d’exercices sur la simplification des fractions :

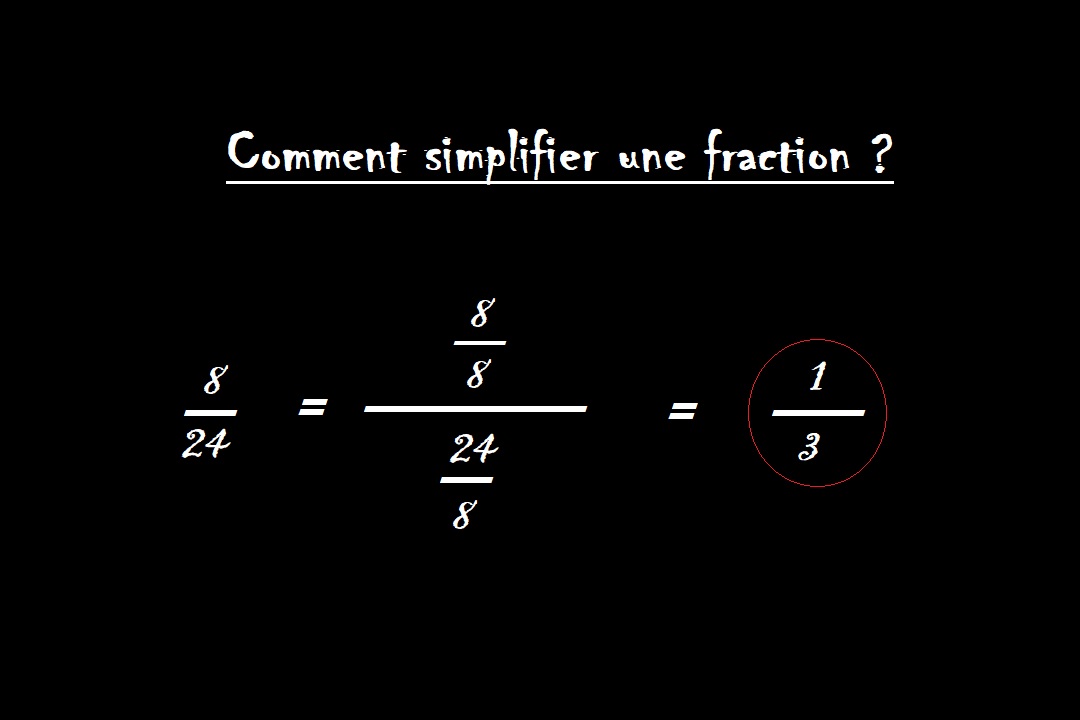
Laisser un commentaire