Comment calculer l’aire d’un triangle ?

Tu veux calculer l’aire d’un triangle et tu te demandes par où commencer ?
Pas besoin de retenir mille formules. On va t’expliquer la méthode la plus simple, avec des exemples pour chaque cas.

L’aire d’un triangle, c’est quoi ?

C’est la surface que la forme occupe, comme si on voulait la colorier entièrement.
On l’exprime en cm², m², etc.

Formule de l’aire d’un triangle

Aire d’un triangle = (Base × Hauteur) ÷ 2

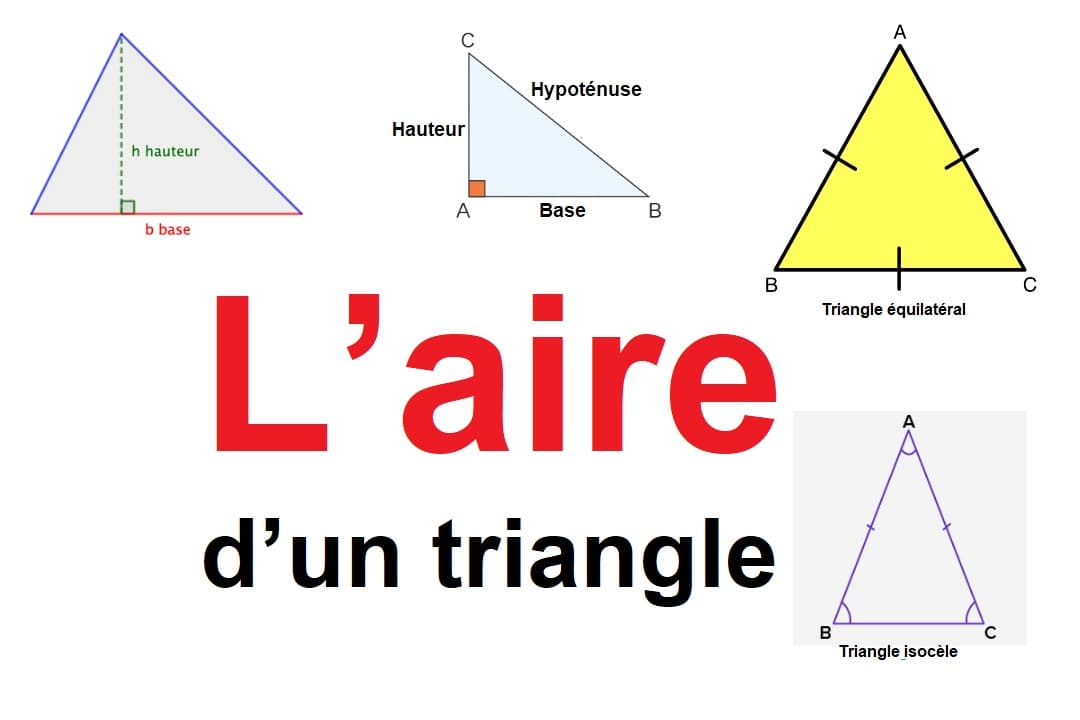
La base est un côté du triangle.
La hauteur est une ligne droite perpendiculaire à cette base, qui touche le sommet opposé.

Exemple :

un triangle de base 10 cm et de hauteur 6 cm :
Aire = (10 × 6) ÷ 2 = 30 cm²

Retenir l’idée : un triangle, c’est la moitié d’un rectangle.

Ce qu’il faut vraiment retenir pour calculer l’aire d’un triangle

Calculer l’aire d’un triangle, ce n’est pas qu’une formule à apprendre. C’est aussi comprendre ce qu’on mesure — une surface — et savoir reconnaître les bons éléments dans la figure.

Formule à retenir

👉 Aire d’un triangle = (Base × Hauteur) ÷ 2
🟡 En version mathématique : A = (B × H) ÷ 2

La base, c’est un côté du triangle.
La hauteur, c’est une ligne perpendiculaire à cette base, qui part du sommet opposé.

💡 Astuce visuelle : il y a 3 hauteurs possibles dans un triangle, selon le côté choisi comme base. Peu importe laquelle on prend, la formule reste valable !

Triangle quelconque, isocèle ou équilatéral : même formule, mêmes gestes

Même si la forme du triangle change, on revient toujours à la même méthode :

Choisir un côté comme base
Identifier (ou tracer) la hauteur perpendiculaire à ce côté
Appliquer la formule

🧮 Exemple : base = 7 cm, hauteur = 4 cm
→ Aire = (7 × 4) ÷ 2 = 14 cm²

🟣 Petit rappel utile :

Triangle quelconque : 3 côtés différents
Triangle isocèle : 2 côtés égaux
Triangle équilatéral : 3 côtés égaux

Même règle, même logique !

Triangle rectangle : la méthode la plus rapide

Bonne nouvelle : pour un triangle rectangle, la base et la hauteur sont déjà là !

Ce sont tout simplement les deux côtés qui forment l’angle droit.

Exemple : AC = 4 cm, BC = 8 cm
→ Aire = (4 × 8) ÷ 2 = 16 cm²

💡 On peut aussi imaginer que ce triangle est la moitié d’un rectangle.
Donc on peut utiliser Aire = (Longueur × Largeur) ÷ 2

Et si on ne connaît pas la hauteur ?

Pas de panique !
Même si la hauteur n’est pas fournie dans l’énoncé, il existe trois façons fiables de calculer l’aire d’un triangle. Il suffit de choisir la méthode qui correspond aux informations qu’on a.

🔹 Tracer la hauteur avec une équerre (la méthode géométrique)

Si tu as un triangle dessiné, tu peux tracer toi-même la hauteur avec une règle et une équerre.

Rappel : La hauteur est une droite perpendiculaire à la base, qui part du sommet opposé.

Comment faire ?

Choisis un côté du triangle comme base.
Pose l’équerre sur ce côté.
Trace une ligne droite perpendiculaire depuis le sommet opposé.

Exemple :
Tu as un triangle avec une base de 6 cm.
Tu traces une hauteur de 5 cm à l’équerre.
Aire = (6 × 5) ÷ 2 = 15 cm²

💡 Cette méthode est idéale en géométrie, quand tu travailles avec des figures tracées.

🔹 Utiliser la formule de Héron (si tu connais les 3 côtés)

Si tu connais les longueurs des trois côtés, même sans hauteur, tu peux utiliser la formule de Héron.

Formule :

Calcule le demi-périmètre :
S = (a + b + c) ÷ 2
Puis applique :
Aire = √[s × (s − a) × (s − b) × (s − c)]

Exemple :
Un triangle a pour côtés : 5 cm, 6 cm et 7 cm

s = (5 + 6 + 7) ÷ 2 = 9
Aire = √[9 × (9 − 5) × (9 − 6) × (9 − 7)]
Aire = √[9 × 4 × 3 × 2] = √216 ≈ 14,7 cm²

💡 Cette méthode est pratique quand aucune hauteur n’est visible, surtout dans des problèmes plus avancés.

🔹 Utiliser la trigonométrie (si tu connais deux côtés et un angle)

Tu as deux côtés et l’angle entre eux ? Parfait : tu peux utiliser une formule avec le sinus.

Formule :
Aire = (a × b × sin(C)) ÷ 2
(a et b sont les côtés, C est l’angle entre eux)

Exemple :
Les côtés mesurent 7 cm et 8 cm, avec un angle de 60° entre eux.

sin(60°) ≈ 0,866
Aire = (7 × 8 × 0,866) ÷ 2 ≈ 24,2 cm²

💡 Cette méthode est utile au secondaire, quand on travaille avec des angles et les fonctions trigonométriques.

Ce qu’il faut retenir

Tu as maintenant toutes les clés pour calculer l’aire d’un triangle, peu importe sa forme.
👉 Le plus important n’est pas de retenir toutes les formules, mais de comprendre l’idée :

Un triangle, c’est la moitié d’un rectangle, et on peut en mesurer l’aire en s’appuyant sur sa base et sa hauteur.

Peu importe le type de triangle, la démarche reste toujours la même :

Identifier ce qu’on connaît (base, hauteur, côtés, angle…)
Choisir la formule adaptée
Poser les bons chiffres au bon endroit

À toi de jouer !

Voici quelques petits défis pour t’entraîner :

Calcule l’aire d’un triangle rectangle dont les côtés perpendiculaires mesurent 6 cm et 4 cm.
Un triangle a une base de 10 cm et une hauteur de 3,5 cm. Quelle est son aire ?
Tu connais les trois côtés d’un triangle : 5 cm, 6 cm et 7 cm. Utilise la formule de Héron.
Et si un triangle équilatéral a des côtés de 8 cm ? Tente la formule spéciale !

Avec ces quelques repères et un peu de pratique, tu verras que calculer une aire, ce n’est pas si compliqué. C’est même assez logique… une fois qu’on a la bonne méthode.