Comment calculer l’aire d’un triangle ?

L’aire d’un triangle est la région qu’il englobe, dans un plan bidimensionnel. Comme nous le savons, un triangle est une forme fermée qui a trois côtés et trois sommets. Ainsi, l’aire d’un triangle est l’espace total occupé par les trois côtés du triangle. Donc, comment calculer l’aire d’un triangle ?

La formule générale pour trouver l’aire du triangle est donnée par la moitié du produit de sa base et de sa hauteur.

En général, le terme « surface » se définit comme la région occupée à l’intérieur des limites d’un objet plat ou d’une figure. En plus, la mesure se fait en unités carrées, l’unité standard étant le mètre carré (m2).

Par ailleurs, pour le calcul de l’aire, il existe des formules prédéfinies pour les carrés, rectangles, cercles, triangles, etc. Dans cet article, nous allons apprendre les formules de calcul de l’aire d’un triangle pour différents types de triangles, ainsi que quelques exemples de problèmes.

Quelle est l’aire d’un triangle ?

L’aire d’un triangle est définie comme la région totale délimitée par les trois côtés d’un triangle donné. Fondamentalement, elle est égale à la moitié de la base multipliée par la hauteur, c’est-à-dire A = ( B × H ) : 2.

Par conséquent, pour trouver l’aire d’un polygone à trois côtés, nous devons connaître sa base (b) et sa hauteur (h).

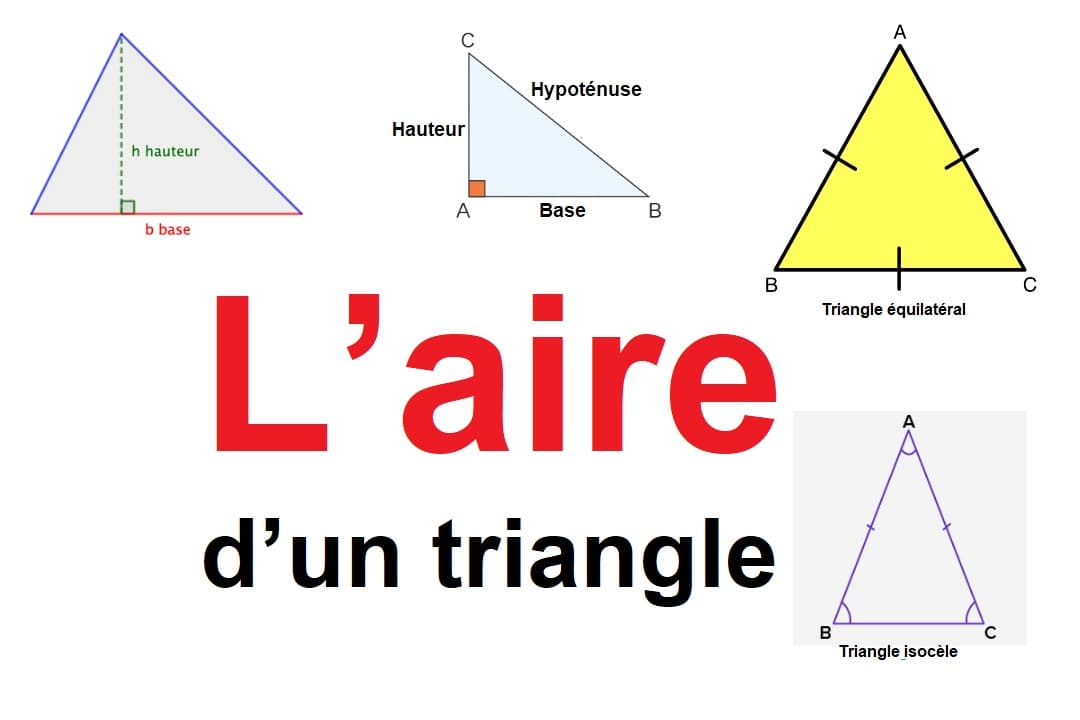
De surcroît, cette méthode s’applique à tous les types de triangles, qu’ils soient scalènes, isocèles ou équilatéraux. A noter aussi que la base et la hauteur du triangle sont perpendiculaires l’une à l’autre. En plus, l’unité d’aire se mesure en unités carrées (m2, cm2)

où B et H sont respectivement la Base et la Hauteur du triangle.

Voyons maintenant comment calculer l’aire d’un triangle à l’aide de la formule donnée. Les formules de calcul de l’aire de tous les différents types de triangles, comme l’aire d’un triangle équilatéral, d’un triangle rectangle, d’un triangle isocèle, ainsi que la façon de trouver l’aire d’un triangle à 3 côtés à l’aide de la formule de Héron, avec des exemples, sont données ci-dessous.

Formule de l’aire d’un triangle :

Aire = (Base × Hauteur) : 2

Exemple

Comment calculer la surface d’un triangle dont la base est B = 3 cm et la hauteur H= 4 cm ?

En utilisant la formule,

Aire d’un triangle, A = (B × H) : 2

= (4 cm × 3 cm) : 2

= 12 cm² : 2

= 6 cm²

Calculer l’aire d’un triangle rectangle

Un triangle rectangle, également appelé triangle droit, a un angle quelconque égal à 90°. Par conséquent, la hauteur du triangle sera la longueur du côté perpendiculaire.

Aire d’un triangle rectangle = A = (Base × Hauteur) : 2

Calculer l’aire d’un triangle équilatéral

Un triangle équilatéral est un triangle dont tous les côtés sont égaux. En plus, la perpendiculaire tracée du sommet du triangle à la base divise la base en deux parties égales. Donc, pour calculer l’aire du triangle équilatéral, il faut connaître la mesure de ses côtés.

Les trois côtés sont égaux ; dans ABC, côtés AB = BC = CA

Aire d’un triangle équilatéral :

A = √3/4 (a)²

Exemple :

A = 4 cm
Donc, A = √3/4 × (4 × 4) cm ²
= 4√3 cm ²

Un triangle équilatéral ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle équilatéral, son aire A est égale à :

A = (B x H) : 2

Calculer l’aire d’un triangle isocèle

Un triangle isocèle a deux de ses côtés égaux et les angles opposés aux côtés égaux sont également égaux.

L’aire d’un triangle isocèle :

Un triangle isocèle ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle isocèle, son aire A est égale à :

A = (B × H) : 2

Comment calculer la base d’un triangle ?

Pour calculer la base d’un triangle connaissant son aire A et sa hauteur h relative à cette base, utilisez la formule de l’aire du triangle :

A= 1/2 b × h.

Réarranger cette formule pour résoudre b :

B = 2 × A / H

Ainsi, si vous avez l’aire et la hauteur, vous pouvez déterminer la longueur de la base en utilisant cette relation.

Exemple :

Imaginons un triangle avec une aire de 20 cm et une hauteur de 5 cm relative à la base que nous cherchons à calculer.

En utilisant la formule B = 2 × A / H, remplaçons A par 20 et h par 5:

B = 2 × A / H

= 2 × 20 cm / 5 cm

= 40 cm / 5 cm

= 8 cm

Ainsi, la longueur de la base de ce triangle est de 8 cm.