Dans cet article, nous allons explorer le théorème de Pythagore, une relation fondamentale entre les côtés d’un triangle rectangle. Nous vous présenterons une série d’exercices qui vous aideront à comprendre et à appliquer ce théorème. Ces exercices vous permettront de développer vos compétences en résolution de problèmes et en visualisation géométrique, tout en renforçant votre compréhension de cette théorie mathématique essentielle. Préparez-vous à plonger dans le monde fascinant du théorème de Pythagore et à relever le défi des exercices qui vous attendent !
C’est quoi le théorème de Pythagore ?
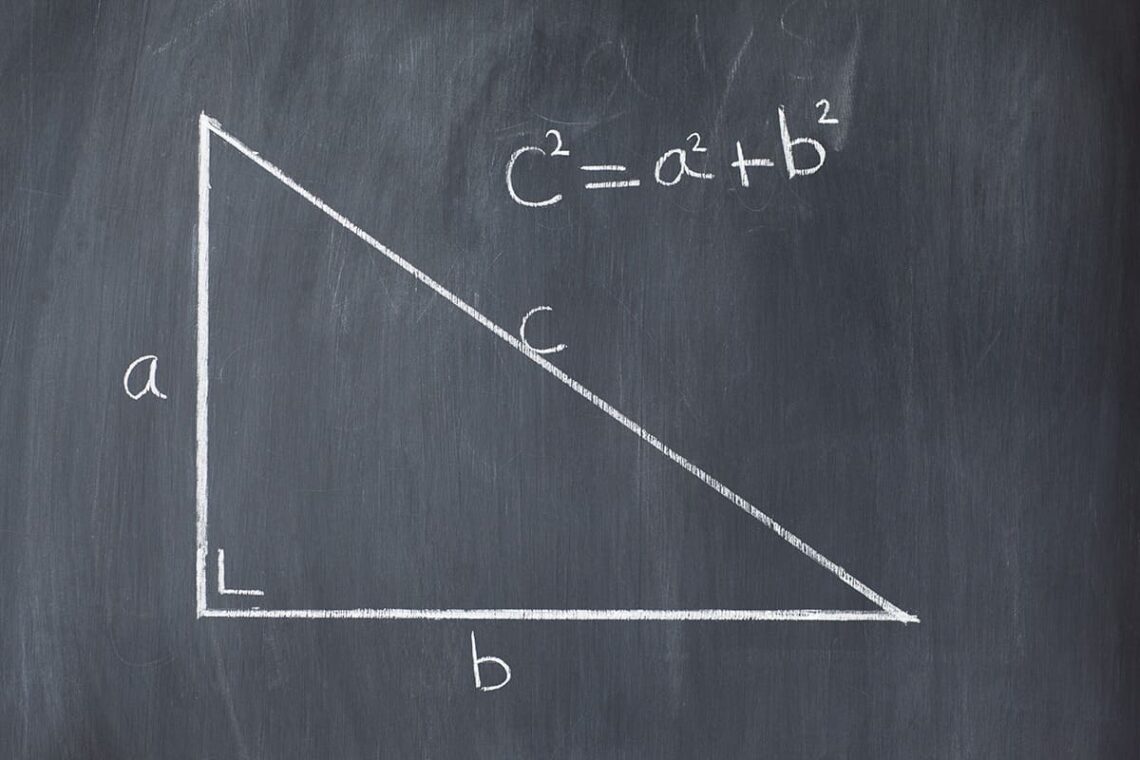
Le théorème de Pythagore affirme que dans un triangle rectangle, la somme des carrés des deux côtés les plus courts du triangle est égale au carré de l’hypoténuse.
En d’autres termes, a2 + b2 = c2
où c représente l’hypoténuse (le côté le plus long) et a et b sont les autres côtés du triangle rectangle.
Que signifie cela ?
Cela signifie que, pour tout triangle rectangle, le carré orange (qui est le carré construit à l’aide du côté le plus long) a la même aire que la somme des deux carrés bleus. Autres formules
Grâce à la formule a2 + b2 = c2, nous pouvons également déduire que :
- b2 = c2 – a2
- a2 = c2 – b2
- c = √(a2 + b2)
- b = √(c2 – a2) et a = √(c2 – b2)
Exercice théorème de Pythagore 4ème
En quatrième, les exercices sur le théorème de Pythagore portent généralement sur la démonstration du théorème, la résolution de problèmes pratiques impliquant des triangles rectangles, ou encore la recherche de valeurs manquantes en utilisant la formule de Pythagore. Ces exercices visent à renforcer la compréhension du théorème et à développer les compétences de calcul et de raisonnement géométrique des élèves.
Fiche 1
Cmath.fr offre une collection d’exercices variés sur le théorème de Pythagore, allant des plus simples aux plus complexes. Les exercices 1 à 4 sont conçus pour développer la compréhension du théorème, tandis que les exercices 5 à 10 permettent son application. Les exercices 11 à 13 proposent des problèmes plus complexes, tandis que les exercices 14 à 16 abordent la réciproque du théorème. Découvrez ces exercices sur ce lien.
Fiche 2
Laprovidence-maths-4eme propose des fichiers PDF téléchargeables comprenant des exercices corrigés sur l’utilisation du théorème de Pythagore avec une calculatrice. Ces fiches sont organisées en différents chapitres et couvrent diverses applications du théorème. Téléchargez ces fiches ici.
Fiche 3
Mathadoc.sésamath et physiques-et-maths proposent tous deux des exercices sur le théorème de Pythagore et sa réciproque. Vous pouvez télécharger ces fiches ici.
Fiche 4
Sur le site physique-et-maths, vous trouverez une série d’exercices mathématiques pour les élèves de 4ème, centrés sur le théorème de Pythagore. Ces exercices couvrent divers sujets tels que le théorème de Pythagore lui-même, la résolution de problèmes, les formes géométriques, les distances, les aires et les dimensions. Ils nécessitent la résolution de problèmes, des calculs, des mesures et des justifications. Téléchargez cette fiche ici.
Fiche 5
Le site Capes de maths propose une série de huit exercices variés sur le théorème de Pythagore. Ces exercices permettent aux élèves de trouver des valeurs manquantes dans des triangles rectangles, de déterminer si un triangle est rectangle et de calculer la longueur d’un côté. Chaque exercice est accompagné d’instructions claires et de schémas, et les corrigés détaillés sont inclus. Téléchargez cette fiche au format PDF ici.
LIRE AUSSI : Calcul théorème de Pythagore
Exercice théorème de Pythagore 3ème
En troisième, les exercices sur le théorème de Pythagore se concentrent sur des problèmes plus complexes, tels que la résolution de triangles rectangles dans des contextes variés, l’application du théorème de Pythagore dans des figures géométriques plus complexes, ou encore l’utilisation du théorème pour calculer des distances ou des longueurs dans des situations réelles. Ces exercices permettent aux élèves de consolider leurs connaissances sur le théorème de Pythagore et de développer leurs compétences en géométrie et en résolution de problèmes.
Exercice théorème de Pythagore 3ème sans correction
Le site « la providence-rochefort » propose une fiche d’exercices stimulante sur le théorème de Pythagore, adaptée aux élèves de 3ème. Cette ressource comprend 2 exercices challengers qui mettront à l’épreuve la compréhension et l’application du théorème, offrant aux élèves une opportunité de renforcer leurs compétences mathématiques. Télécharger cette fiche.
Sur le site mathsdouville.e-monsite, découvrez une fiche d’exercices complète sur le théorème de Pythagore spécialement conçue pour les élèves de 3ème. Cette ressource propose 11 exercices variés et stimulants qui encouragent les élèves à appliquer le théorème dans différents contextes géométriques, permettant ainsi de renforcer leur compréhension et leur maîtrise de ce concept mathématique fondamental. Télécharger cette fiche.
Le site maths-sciences met à disposition une fiche d’exercices riche sur le théorème de Pythagore, conçue pour les élèves de 3ème. Cette ressource propose 12 exercices variés qui mettent en pratique le théorème dans différents contextes géométriques, offrant aux élèves une opportunité d’améliorer leur compréhension et leur résolution de problèmes liés à ce concept mathématique clé. Télécharger cette fiche.
Sur le site clg-arausio.ac-aix-marseille, découvrez une fiche d’exercices complète sur le théorème de Pythagore, spécialement conçue pour les élèves de 3ème. Cette ressource propose 4 exercices variés accompagnés de corrections détaillées, permettant aux élèves de consolider leurs compétences en résolution de problèmes utilisant ce théorème clé en géométrie. Télécharger cette fiche.
Exercice théorème de Pythagore 3ème avec correction
La fiche d’exercice sur le théorème de Pythagore de maths.bzh propose cinq exercices variés pour les élèves de 3ème. Chaque exercice aborde une situation géométrique spécifique et permet de calculer des longueurs manquantes ou des côtés de triangles en utilisant le théorème de Pythagore. Des corrections détaillées sont fournies pour chaque exercice. C’est un outil pédagogique pratique pour renforcer la compréhension et l’application du théorème de Pythagore. Télécharger cette fiche.
Cette fiche d’exercice, disponible sur le site mathsdouville, propose 11 exercices variés pour aider les élèves de 3ème à pratiquer le théorème de Pythagore. Chaque exercice est accompagné d’une correction détaillée pour faciliter l’apprentissage et la compréhension. Télécharger cette fiche.
Sur le site académie-poitiers.fr, découvrez une fiche d’exercices complète sur le théorème de Pythagore destinée aux élèves de 3ème. Cette ressource propose 7 exercices variés et stimulants, accompagnés d’une correction détaillée pour aider les élèves à consolider leur compréhension de ce concept mathématique essentiel. Télécharger cette fiche.
Le site académie-Lyon.fr vous offre une fiche d’exercices ciblée sur le théorème de Pythagore, spécialement conçue pour les élèves de 3ème. Avec 5 exercices pertinents et variés, accompagnés d’une correction détaillée, cette ressource permet aux élèves de consolider leurs compétences en utilisant ce théorème fondamental de la géométrie. Télécharger cette fiche.
Le site melusine.eu.org propose une fiche d’exercices complète sur le théorème de Pythagore, spécialement conçue pour les élèves de 3ème. Cette ressource comprend 6 exercices variés qui permettront aux élèves de consolider leur compréhension et leur application de ce théorème, avec une correction détaillée pour un apprentissage optimal. Télécharger cette fiche.
LIRE AUSSI : Tables de Pythagore à imprimer
Exercices sur le théorème de Pythagore avec correction
Découvrez ces exercices captivants basés sur le célèbre théorème de Pythagore, vous permettant d’explorer les relations entre les côtés d’un triangle rectangle. Testez vos compétences en calculant les longueurs d’hypoténuse et de côtés à travers des situations variées, renforçant ainsi votre compréhension pratique de ce théorème fondamental de la géométrie.
Exercice 1
Un triangle rectangle a un côté de longueur 5 cm et un côté de longueur 12 cm. Trouvez la longueur de l’hypoténuse.
Solution :
Pour trouver la longueur de l’hypoténuse, nous utilisons le théorème de Pythagore. Soit : a = 5 cm et b = 12 cm.
On a : c² = a² + b²
c² = 5² + 12²
= 25 + 144
c² = 169
En prenant la racine carrée des deux côtés, on obtient : c = √169 = 13 cm
La longueur de l’hypoténuse est de 13 cm.
Exercice 2
Un triangle a un côté de longueur 7 cm, un autre côté de longueur 24 cm et un angle de 90 degrés entre ces deux côtés. Calculez la longueur du troisième côté.
Solution :
Nous utilisons encore une fois le théorème de Pythagore. Soit : a = 7 cm et b = 24 cm.
On a : c² = a² + b²
c² = 7² + 24²
= 49 + 576
c² = 625
En prenant la racine carrée des deux côtés, on obtient : c = √625 = 25 cm
Donc, la longueur du troisième côté est de 25 cm.
Exercice 3
Dans un triangle rectangle, l’hypoténuse mesure 13 cm et l’un des côtés a une longueur de 5 cm. Trouvez la longueur du troisième côté.
Solution :
Dans ce cas, nous avons l’hypoténuse c = 13 cm et l’un des côtés a = 5 cm. Nous devons trouver la longueur du troisième côté, b.
On utilise le théorème de Pythagore : b² = c² – a²
b² = 13² – 5²
= 169 – 25
b²= 144
En prenant la racine carrée des deux côtés, on obtient : b = √144 = 12 cm
Donc, la longueur du troisième côté est de 12 cm.
Exercice 4
Un triangle a des côtés de longueur 9 cm, 12 cm et 15 cm. Est-ce un triangle rectangle ?
Solution :
Pour déterminer si le triangle est rectangle, nous vérifions si la somme des carrés des deux côtés les plus courts est égale au carré de l’hypoténuse.
Dans ce cas, nous avons : a = 9 cm, b = 12 cm et c = 15 cm.
Calculons :
a² + b² = 9² + 12²
= 81 + 144
= 225
Et
c² = 15² = 225
Comme a² + b² = c², le triangle est rectangle.
Exercice 5
Un triangle rectangle a un côté de longueur 8 cm et un autre côté de longueur 15 cm. Calculez la longueur de l’hypoténuse.
Solution :
Nous appliquons le théorème de Pythagore avec a = 8 cm et b = 15 cm.
On a : c² = a² + b²
c² = 8² + 15²
= 64 + 225
c² = 289
En prenant la racine carrée des deux côtés, on obtient : c = √289 = 17 cm
Donc, la longueur de l’hypoténuse est de 17 cm.
Exercice 6
Un triangle rectangle a un côté de longueur 3 cm et l’hypoténuse mesure 5 cm. Calculez la longueur du côté manquant.
Solution :
Pour trouver la longueur du côté manquant, nous utilisons le théorème de Pythagore. Soit l’hypoténuse c = 5 cm et l’un des côtés a = 3 cm.
On a : b² = c² – a²
b² = 5² – 3²
= 25 – 9
b² = 16
En prenant la racine carrée des deux côtés, on obtient : b = √16 = 4 cm
Donc, la longueur du côté manquant est de 4 cm.
Exercice 7
Dans un triangle rectangle, l’hypoténuse mesure 17 cm et l’un des côtés a une longueur de 8 cm. Trouvez la longueur du troisième côté.
Solution :
Dans ce cas, nous avons l’hypoténuse c = 17 cm et l’un des côtés : a = 8 cm. Nous devons trouver la longueur du troisième côté, b.
On utilise le théorème de Pythagore : b² = c² – a²
b² = 17² – 8²
= 289 – 64
b² = 225
En prenant la racine carrée des deux côtés, on obtient : b = √225 = 15 cm
Donc, la longueur du troisième côté est de 15 cm.
Exercice 8
Un triangle a un côté de longueur 10 cm et un autre côté de longueur 8 cm. Est-ce un triangle rectangle ? Si oui, calculez la longueur de l’hypoténuse.
Solution :
Pour déterminer si le triangle est rectangle, nous vérifions si la somme des carrés des deux côtés les plus courts est égale au carré de l’hypoténuse.
Dans ce cas, nous avons : a = 10 cm et b = 8 cm.
Calculons : a² + b² = 10² + 8² = 100 + 64 = 164
Et c² = 12² = 144
Comme a² + b² n’est pas égal à c², le triangle n’est pas rectangle.
Exercice 9
Un triangle rectangle a un côté de longueur 9 cm et l’hypoténuse mesure 15 cm. Trouvez la longueur du côté manquant.
Solution :
Pour trouver la longueur du côté manquant, nous utilisons le théorème de Pythagore. Soit l’hypoténuse c = 15 cm et l’un des côtés a = 9 cm.
On a : b² = c² – a²
b² = 15² – 9²
= 225 – 81
b² = 144
En prenant la racine carrée des deux côtés, on obtient : b = √144 = 12 cm
Donc, la longueur du côté manquant est de 12 cm.
Exercice 10
Un triangle a des côtés de longueur 5 cm, 12 cm et x cm. Est-ce un triangle rectangle ? Si oui, calculez la valeur de x.
Solution :
Pour déterminer si le triangle est rectangle, nous vérifions si la somme des carrés des deux côtés les plus courts est égale au carré de l’hypoténuse.
Dans ce cas, nous avons : a = 5 cm, b = 12 cm et c = x cm.
Calculons : a² + b² = 5² + 12² = 25 + 144 = 169
Et c² = x²
Comme a² + b² n’est pas égal à c², le triangle n’est pas rectangle.

Laisser un commentaire